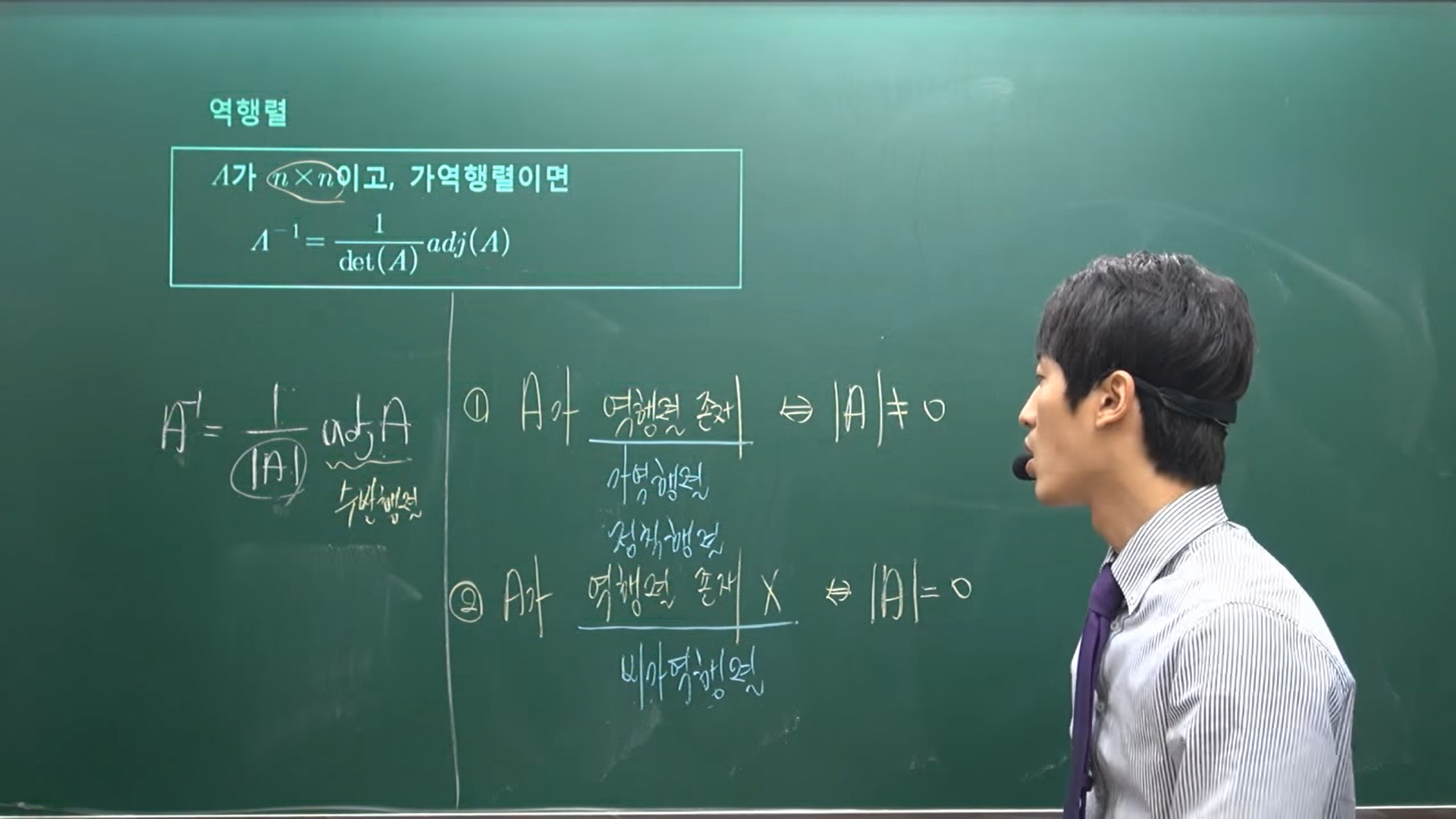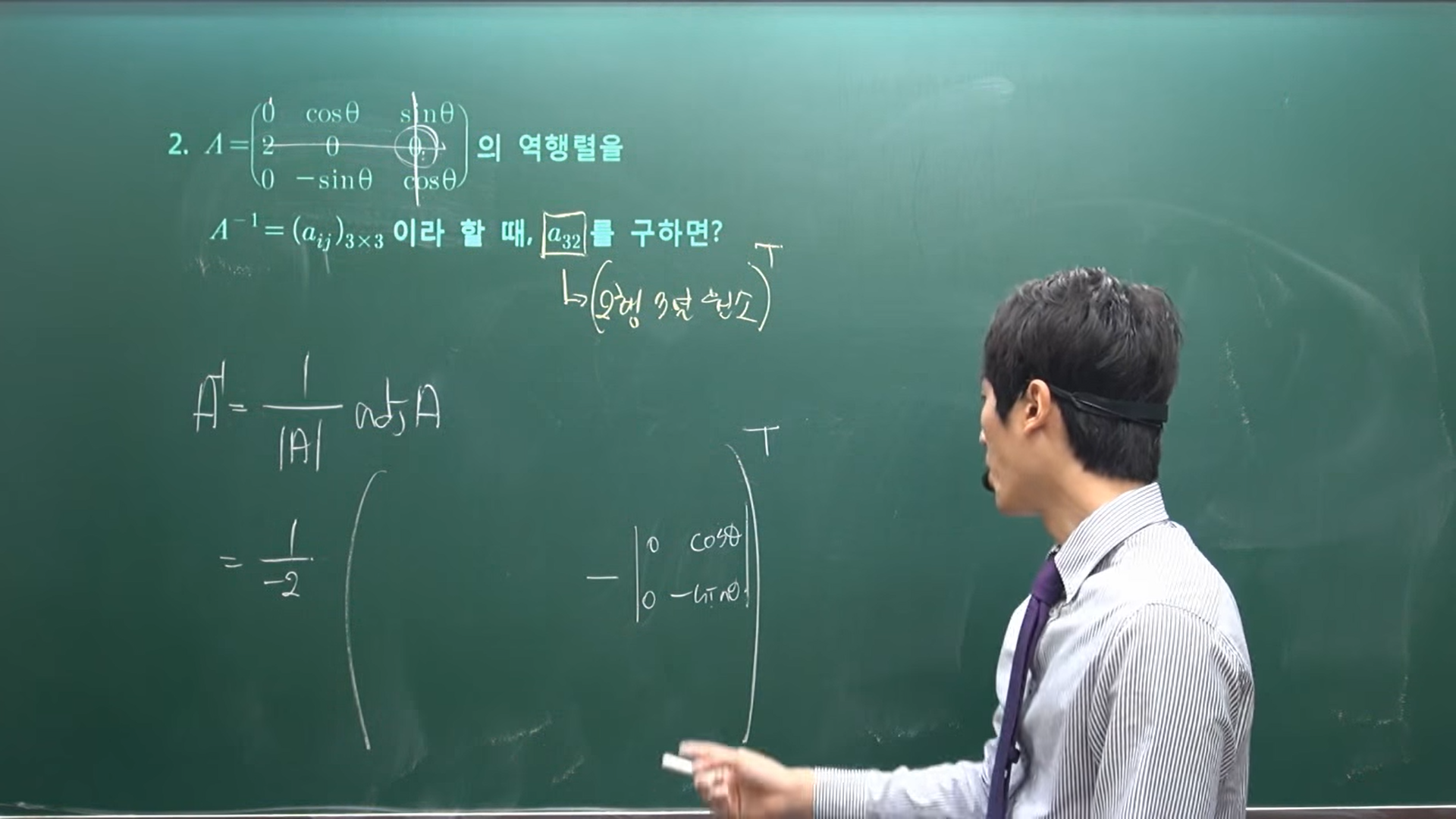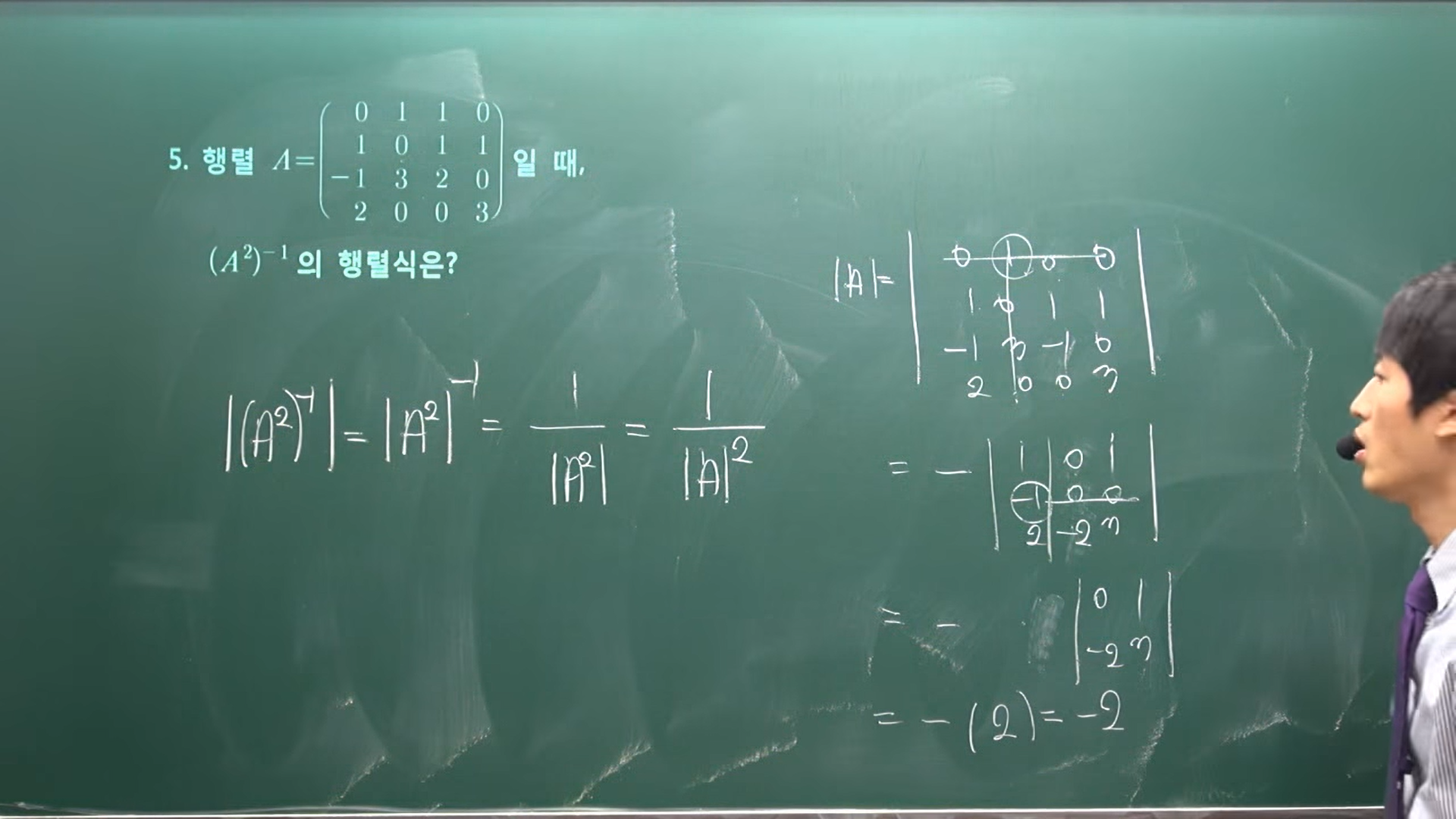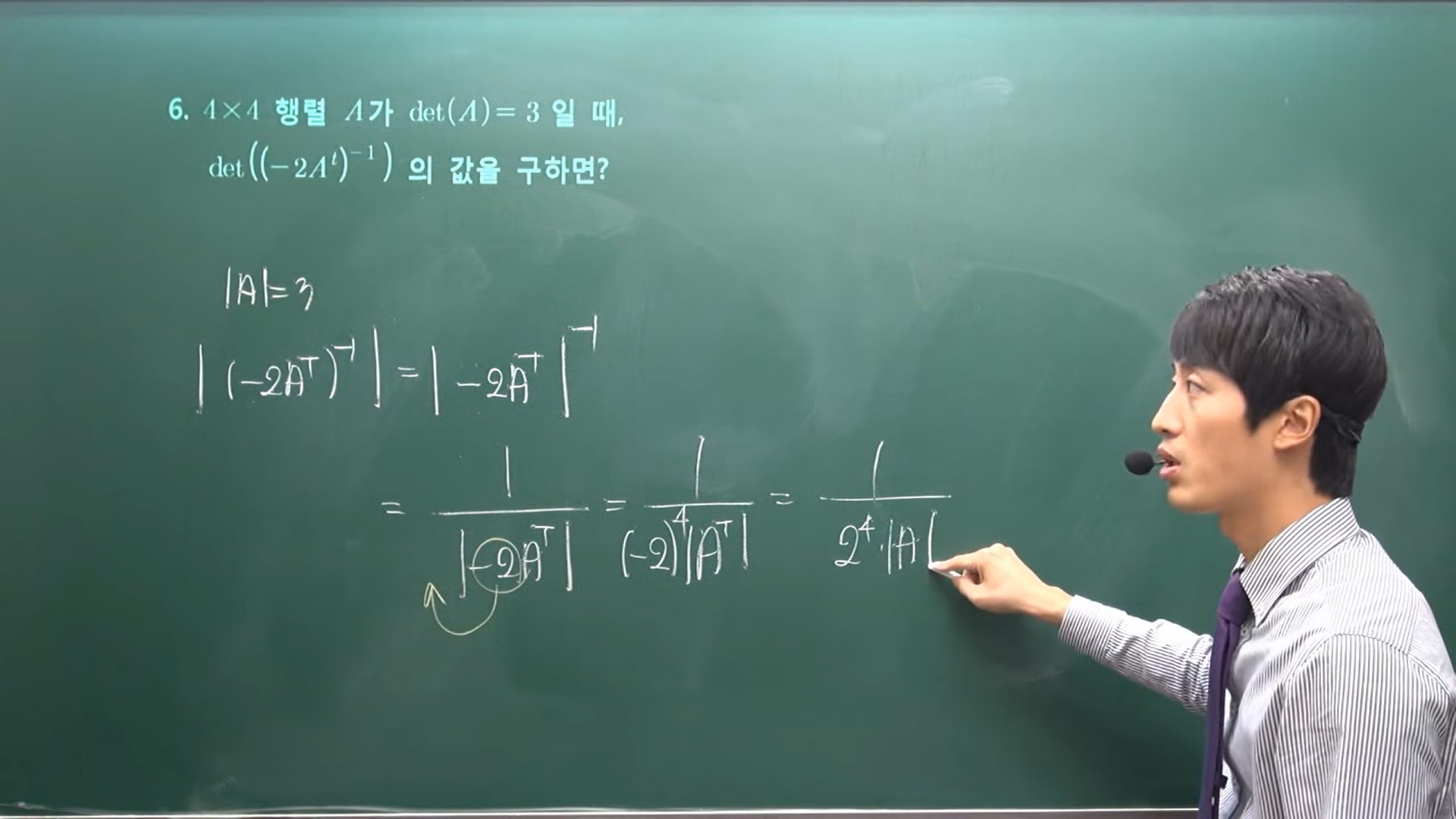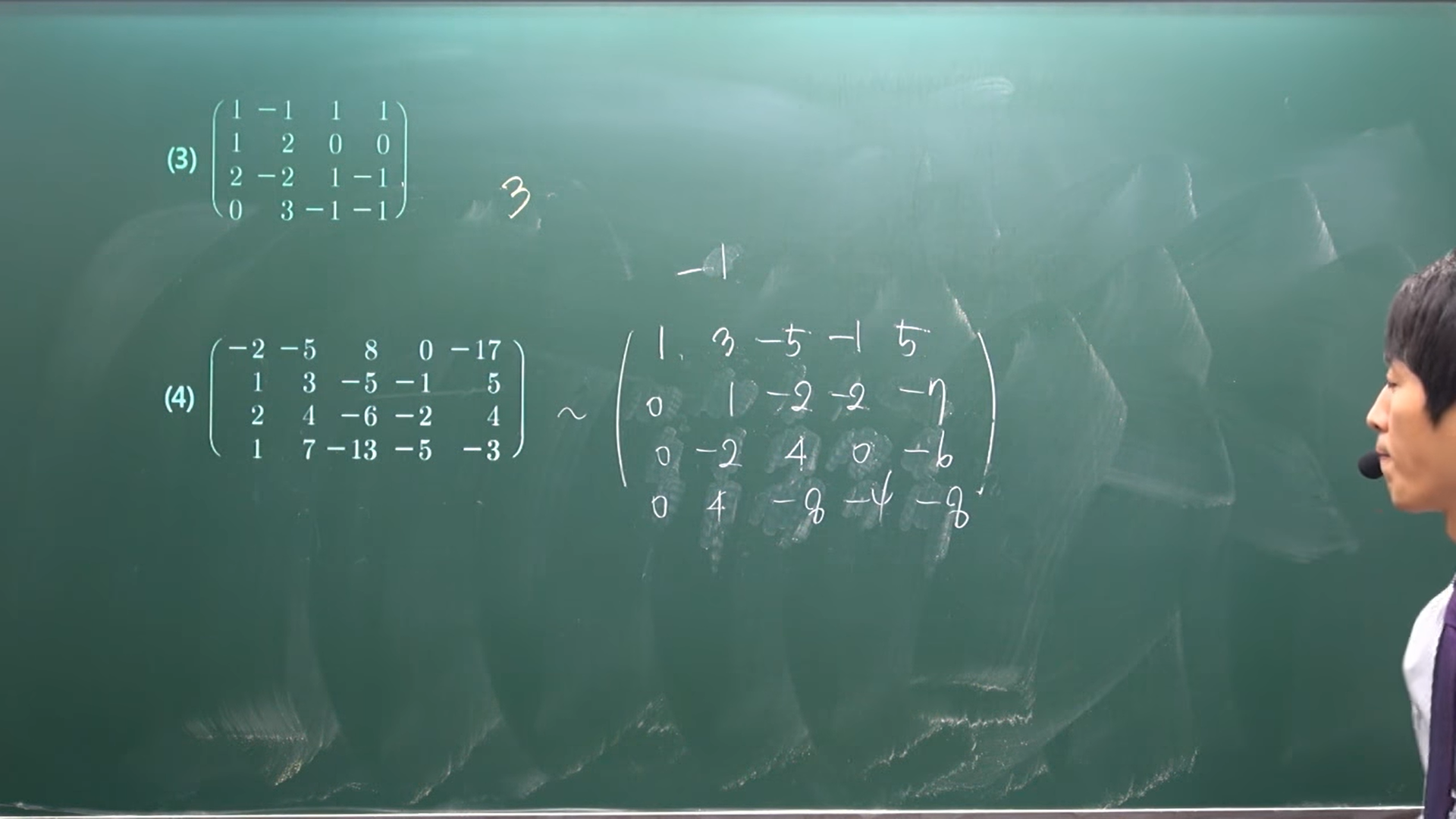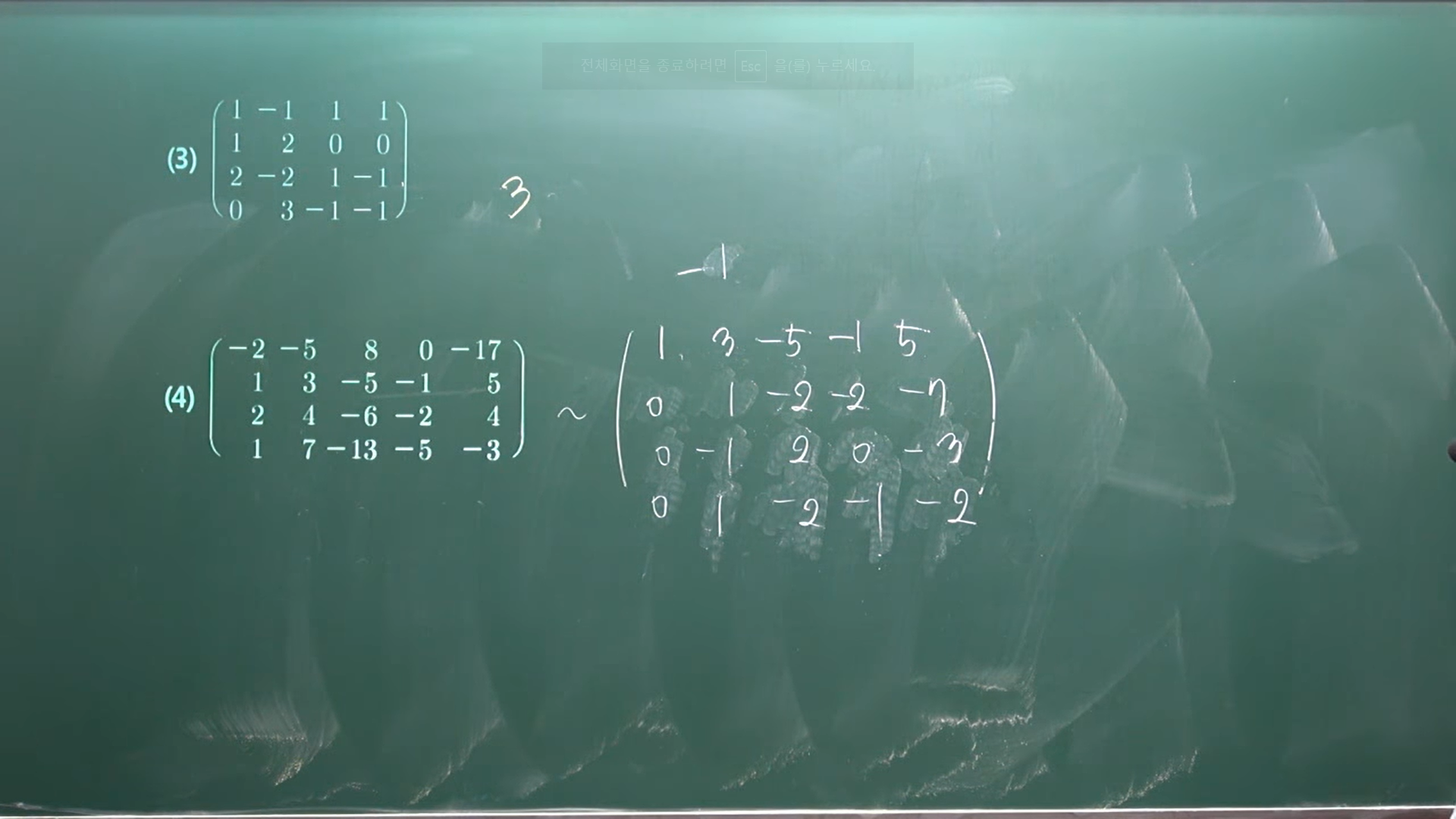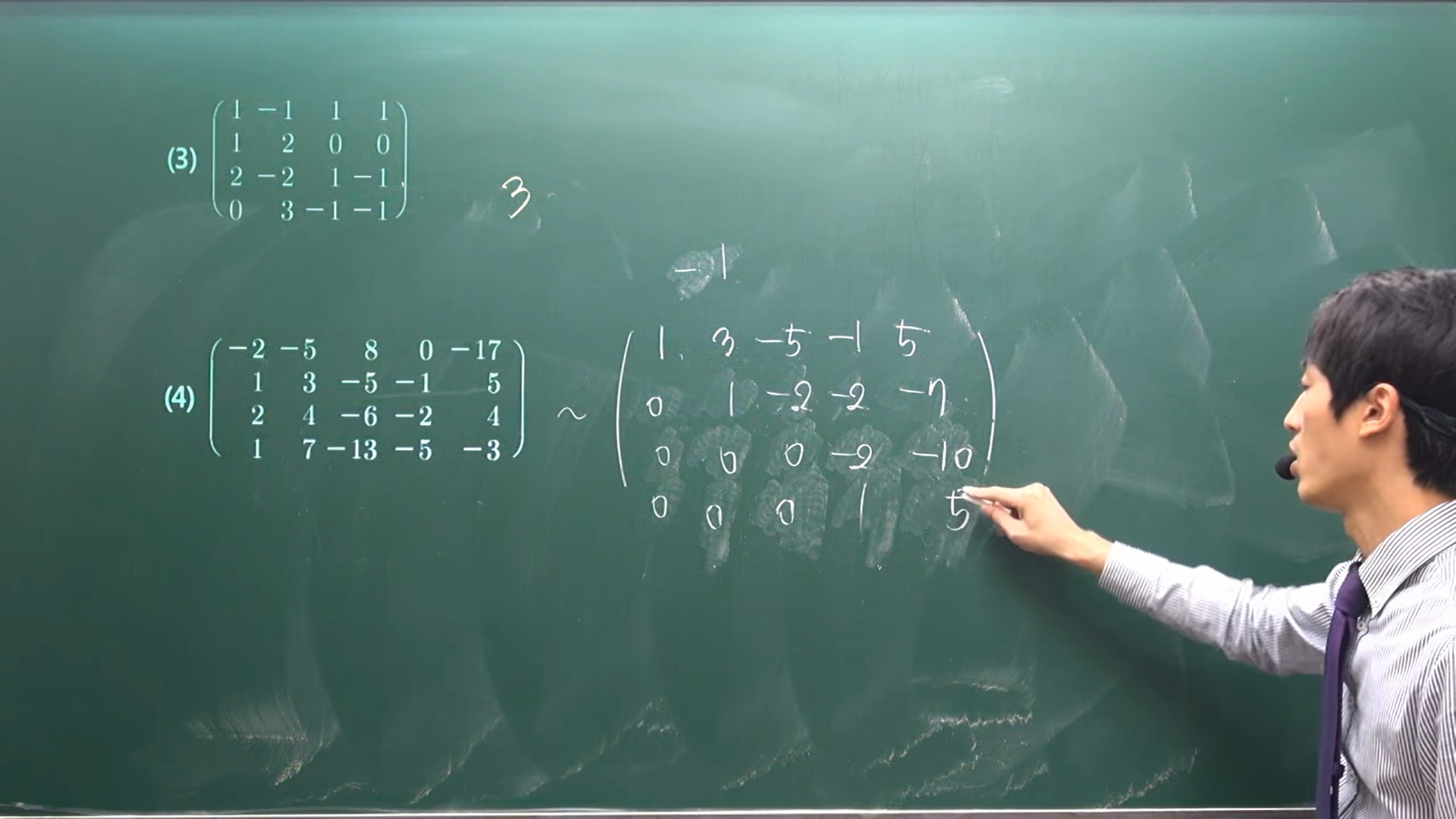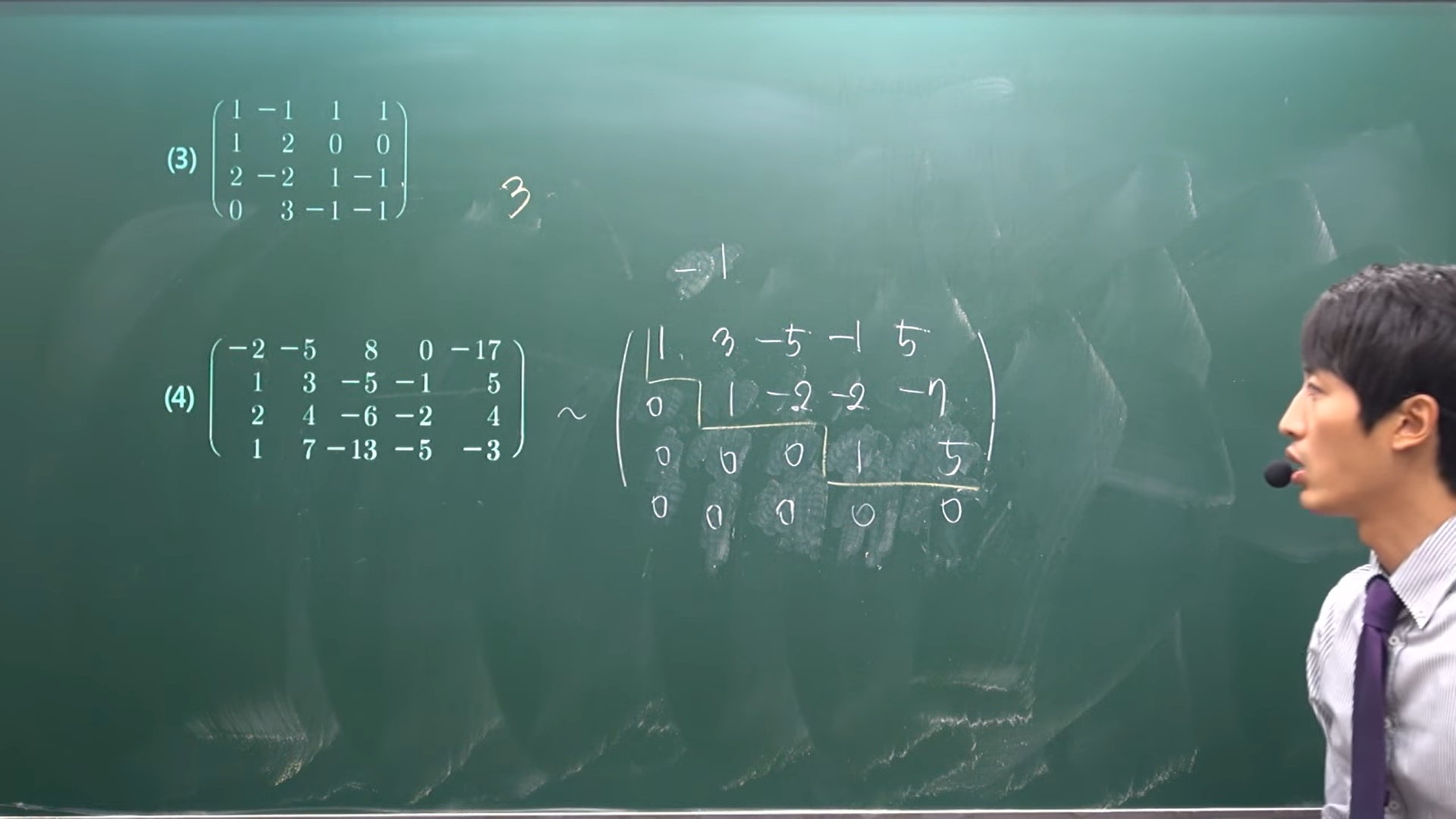1. OT

장소: 포스코 국제관

일시: 11월 1일 오후 4시

 

3시 40분쯤 도착해서 체크인을 하고

숙소로 올라갔다

 

 

보면서 룸메랑 안 맞으면 진짜 9주가

불편하겠다는 생각을 했다

(나는 다행히도 잘 맞는 듯!)

 

OT 때 작성해야하는 서류가 많기 때문에

꼭 필기류를 지참해서 

OT 장소로 가길 바란다!

 

 

2. OT 이후

 

교육관과 식당을 미리 찾아보러

룸메와 산책을 나갔다

 

지도로 찍고 가는 걸 추천한다

어어어엄청 넓다!!

(참고로 국제관에서 나와서 오른쪽에

시계가 있는 건물로 가로질러서 가면 편함)

 

산책을 끝내고

룸메랑 수학 사전 강의를 같이 듣기 위해

박태준 학술 정보관에서 공부를 하고

10시쯤 숙소에 복귀해

담소를 나누고

내일을 위해 잠들었다!

 

너무 기대된다!

빨리 팀원들이랑 만나서 친해졌으면!

 

'교육 프로그램 후기 > 포스코 AI&BigData 아카데미 후기' 카테고리의 다른 글

청년 AI · Big Data 아카데미 12기 - 빅데이터 과정  (4) 2021.02.09
청년 AI · Big Data 아카데미 12기 - 2일차  (0) 2020.11.04
청년 AI · Big Data 아카데미 12기 - 1일차  (3) 2020.11.03
포스코 AI·빅데이터 아카데미 0일차 - 2차 면접 및 최종 합격  (2) 2020.11.02
포스코 AI·빅데이터 아카데미 0일차 - 지원 및 1차 서류 합격  (0) 2020.11.02
저렇게 생겨먹은 모양을 일차결합이라고 한다 일차결합을 계산해서 나온 결과값을 생성이라고 한다
  실수배(저기서는 2배, 1/2배)하여 만들어낼 수 있으면
종속적인 관계이다(불필요한 존재가 있는 것)

또한 실수배하여 더하거나 빼서 나올 수 있어도
종속적인 관계이다

 

문제 1  
실수배 != x배
문제 2  
 
문제 3  
  cos, sin, tan를 더해서 만들 수 있기 때문에
sec는 불필한 존재가 된다
 
문제 4  
벡터가 무수히 많을 때 편하게 종속과 독립을 구별하기 
위한 방법 (행렬식) - 정방 행렬일 때		 벡터가 무수히 많을 때 편하게 종속과 독립을 구별하기 
위한 방법 (랭크) - 정방 행렬이 아닐 때
  ㄷ. 여기서 일차독립 최대 개수는 rank A = 2개이다
ㄹ. 위 3개는 서로 독립의 관계를 가진다

 

문제 5  
 
문제 6 선형 독립인 벡터들의 최대 개수 = rank A 개수 == 3  
 

 

  
음악(벡터 공간)의 도레미파솔라시도 = 기저
프린터(벡터 공간)의 빨,초, 파, 검 = 기저		  

 

문제 1 (가)  
 

'Memo > 포스코 AI&BD 사전학습' 카테고리의 다른 글

선형 대수 - 8강 기저 및 차원  (0) 2020.11.04
선형 대수 - 7강 벡터 공간 및 부분 공간  (0) 2020.11.03
선형대수 - 6강 역행렬  (0) 2020.11.02
선형대수 - 5강 랭크의 활용  (0) 2020.11.02
선형대수 - 4강 랭크  (0) 2020.11.02
  8가지 성질 중에 (1),(2),(3)을 집중해서 보면 된다
  zero 벡터의 존재 유무에 따라 벡터 공간인지 아닌지를
걸러낼 수 있는 좋은 기준이 된다

 

집합 -> 공간 -> 벡터 공간을 정의하는데 있어서
     2가지    8가지 조건들이 필요했다.		  
크림빵에서 빵을 뜯어냈을 때 크림이 있다면 그 빵은
크림빵이고, 크림이 없다면 빵이다
벡터 공간에서도 공간을 뜯어냈을 때
벡터 공간의 8가지 성질을 만족한다면 부분 공간이라고
하는 것이다. 		 원점을 지나가야지만 제로 벡터가 존재하는 것이다
왜냐하면 제로 벡터가 존재하기 위해서는 무조건 원점을
지나야 하기 때문이다
  저기서 dot는 내적을 의미한다
모두 직교하기 때문에 내적했을 때 0이 된다  
 
어떤 벡터공간 V에서
0과 자기 자신은 반드시 그 집합, 그 공간의
부분 공간이 될 수 있다

부분 공간이 될려면 반드시 0이 있어야 한다 {0}
덧셈에 닫혀있어야 하기 때문에  0+0 = 0
실수배 3*0 = 0

자기 자신은 벡터 공간이자 부분 공간이 될 수 있다
ㄱ,ㄴ: 뿐이다 때문에 틀렸다
ㄷ: R^2의 원점을 지나는 모든 직선이 없어서!

#주의#
R^3의 부분 공간은
{0}, R^3, 원점을 지나가는 직선, 원점을 지나가는 평면이다.

 

'Memo > 포스코 AI&BD 사전학습' 카테고리의 다른 글

선형 대수 - 8강 기저 및 차원  (0) 2020.11.04
선형대수 - 8강 일차 종속 및 독립  (0) 2020.11.03
선형대수 - 6강 역행렬  (0) 2020.11.02
선형대수 - 5강 랭크의 활용  (0) 2020.11.02
선형대수 - 4강 랭크  (0) 2020.11.02
adj(A)는 수반 행렬이라 명칭한다  
  수반행렬의 1열을 물어보면 전치하기 전에 1행을
수반행렬의 1행을 물어보면 전치하기 전에 1열을 계산

 
 
가역행렬: 역행렬이 있는 행렬(정칙행렬) 전치X
비가역행렬: 역행렬이 존재하지 않는 행렬		  

 

문제 1
첫 번째 열의 성분 -> 전치하기 전의 첫 번째 행		  
 
문제 2
a32 -> 전치하기 전의 a23		  
 
문제 3
3행 원소들의 합 -> 전치하기 전의 3열 원소들의 합		  
!!!하삼각 행렬의 행렬식은 주 대각선 원소만 곱하면 된다  
문제 4
역행렬을 갖지 않는다 == 행렬식의 값이 0이다		  
 

 

역행렬의 성질  
성질 (6) 성질 (7)

 

문제 5  
따라서 1/4
문제 6  
문제 7  
 
문제 8  
 
상삼각행렬의 행렬식은 대각선의 곱이다  
문제 9  
문제 10  
 

 

문제 11  
 
문제 12  
 
(b)에 의해 참임을 증명했기 때문에 (c)도 참이다  

 

'Memo > 포스코 AI&BD 사전학습' 카테고리의 다른 글

선형대수 - 8강 일차 종속 및 독립  (0) 2020.11.03
선형 대수 - 7강 벡터 공간 및 부분 공간  (0) 2020.11.03
선형대수 - 5강 랭크의 활용  (0) 2020.11.02
선형대수 - 4강 랭크  (0) 2020.11.02
선형대수 - 3강 행렬식1,2  (0) 2020.11.01
x1, x2, x3 처럼 3개를 의미하는 것처럼 미지수 개수: n 오른쪽이 0이면 선형이라는 표현을 사용한다

 

 성질 (1)
계수 행렬 A rank 개수와 확대 행렬의 rank 개수보다 작으면
해가 존재하지 않는다

성질 (2)
계수 행렬 A rank 개수와 확대 행렬의 rank 개수보다 같으면
해가 오직 하나 존재한다 (유일한 해를 가진다)

성질 (3)
계수 행렬 A rank 개수와 확대 행렬의 rank 개수보다 크면
무수히 많은 해를 가진다 (~이외의 해를 가진다)
암기하래...  

 

문제 1  
 
문제 2  
문제 3  
선형 연립 방정식이면 
rank(A)와 rank(A|B)는 같을 수 밖에 없다		 A가 nxn 행렬일 때
(1)행렬식 값이 0이 아니면 rank(A) = n이고
(2)행렬식 값이 0이면 rank(A) < n이다
<행렬식 값이 0일 때> <행렬식 값이 0이 아닐 때>

 

문제 4  
 
문제 5  
  오른쪽 예에서 a가 0이면 1이 선두가 되기 때문에
b가 사라져야 하므로 a != 0의 조건을 포함하고 있어야 한다
 

 

문제 6 답: -3a-b+c=0  
  해가 존재할 조건 : 해가 1개일 때 + 해가 무수히 많을 때
 
문제 7  
앞에 있는 숫자를 최소 공배수로 맞추어도 상관 없다  

 

문제 8  
문제 9  

'Memo > 포스코 AI&BD 사전학습' 카테고리의 다른 글

선형 대수 - 7강 벡터 공간 및 부분 공간  (0) 2020.11.03
선형대수 - 6강 역행렬  (0) 2020.11.02
선형대수 - 4강 랭크  (0) 2020.11.02
선형대수 - 3강 행렬식1,2  (0) 2020.11.01
선형대수 - 2강 벡터의 내적  (0) 2020.11.01

 

랭크는 연립 방정식과 성질이 비슷하다 rank: 0이 아닌 줄의 개수
  행을 바꿔도 괜찮다
0이 아닌 실수배를 해도 괜찮다

 

문제 (1) rank(A) = 3  
  가우스 소거법
첫 번째(선두) 행이 0이 아닌 숫자 밑은 다 0이어야 한다.
두 번째 행에 0이 아닌 숫자 밑은 다 0이어야 한다.

계단 형식으로 내려간다
문제 (2) rank(A) = 2  
문제 (3) rank(A) = 3  
문제 (4) rank(A) = 3  
 
문제 (5) rank(A) = 2  
문제 (6) rank(A) = 3  

 

'Memo > 포스코 AI&BD 사전학습' 카테고리의 다른 글

선형대수 - 6강 역행렬  (0) 2020.11.02
선형대수 - 5강 랭크의 활용  (0) 2020.11.02
선형대수 - 3강 행렬식1,2  (0) 2020.11.01
선형대수 - 2강 벡터의 내적  (0) 2020.11.01
선형대수 - 1강 벡터의 정의  (0) 2020.11.01

+ Recent posts

티스토리툴바