 |
 |
 |
 |
| x1, x2, x3 처럼 3개를 의미하는 것처럼 미지수 개수: n | 오른쪽이 0이면 선형이라는 표현을 사용한다 |
 |
성질 (1) 계수 행렬 A rank 개수와 확대 행렬의 rank 개수보다 작으면 해가 존재하지 않는다 성질 (2) 계수 행렬 A rank 개수와 확대 행렬의 rank 개수보다 같으면 해가 오직 하나 존재한다 (유일한 해를 가진다) 성질 (3) 계수 행렬 A rank 개수와 확대 행렬의 rank 개수보다 크면 무수히 많은 해를 가진다 (~이외의 해를 가진다) |
| 암기하래... |
| 문제 1 | |
 |
 |
 |
|
| 문제 2 | |
 |
 |
| 문제 3 | |
 |
 |
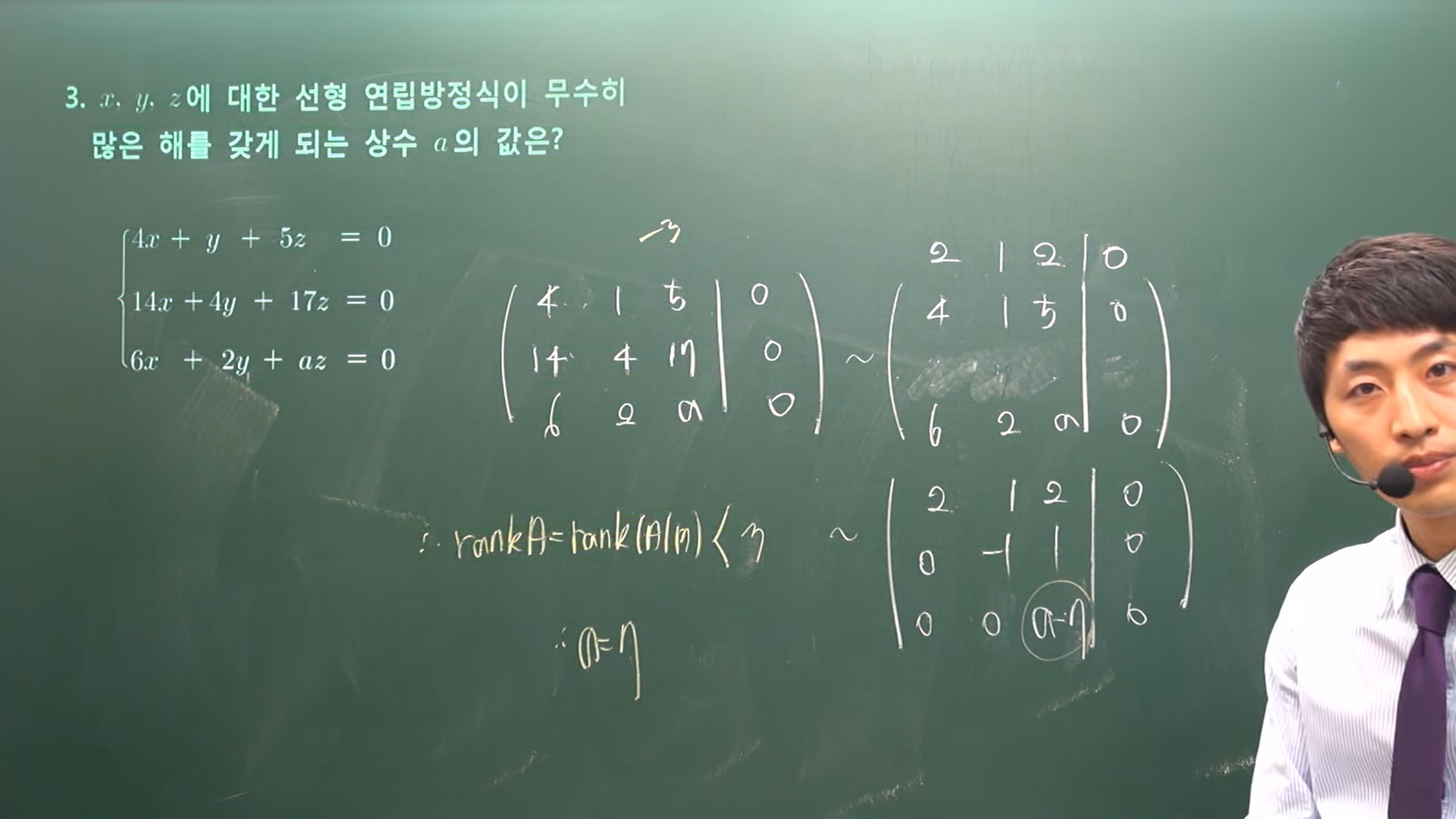 |
 |
| 선형 연립 방정식이면 rank(A)와 rank(A|B)는 같을 수 밖에 없다 |
A가 nxn 행렬일 때 (1)행렬식 값이 0이 아니면 rank(A) = n이고 (2)행렬식 값이 0이면 rank(A) < n이다 |
 |
 |
| <행렬식 값이 0일 때> | <행렬식 값이 0이 아닐 때> |
| 문제 4 | |
 |
|
| 문제 5 | |
 |
 |
| 오른쪽 예에서 a가 0이면 1이 선두가 되기 때문에 b가 사라져야 하므로 a != 0의 조건을 포함하고 있어야 한다 |
|
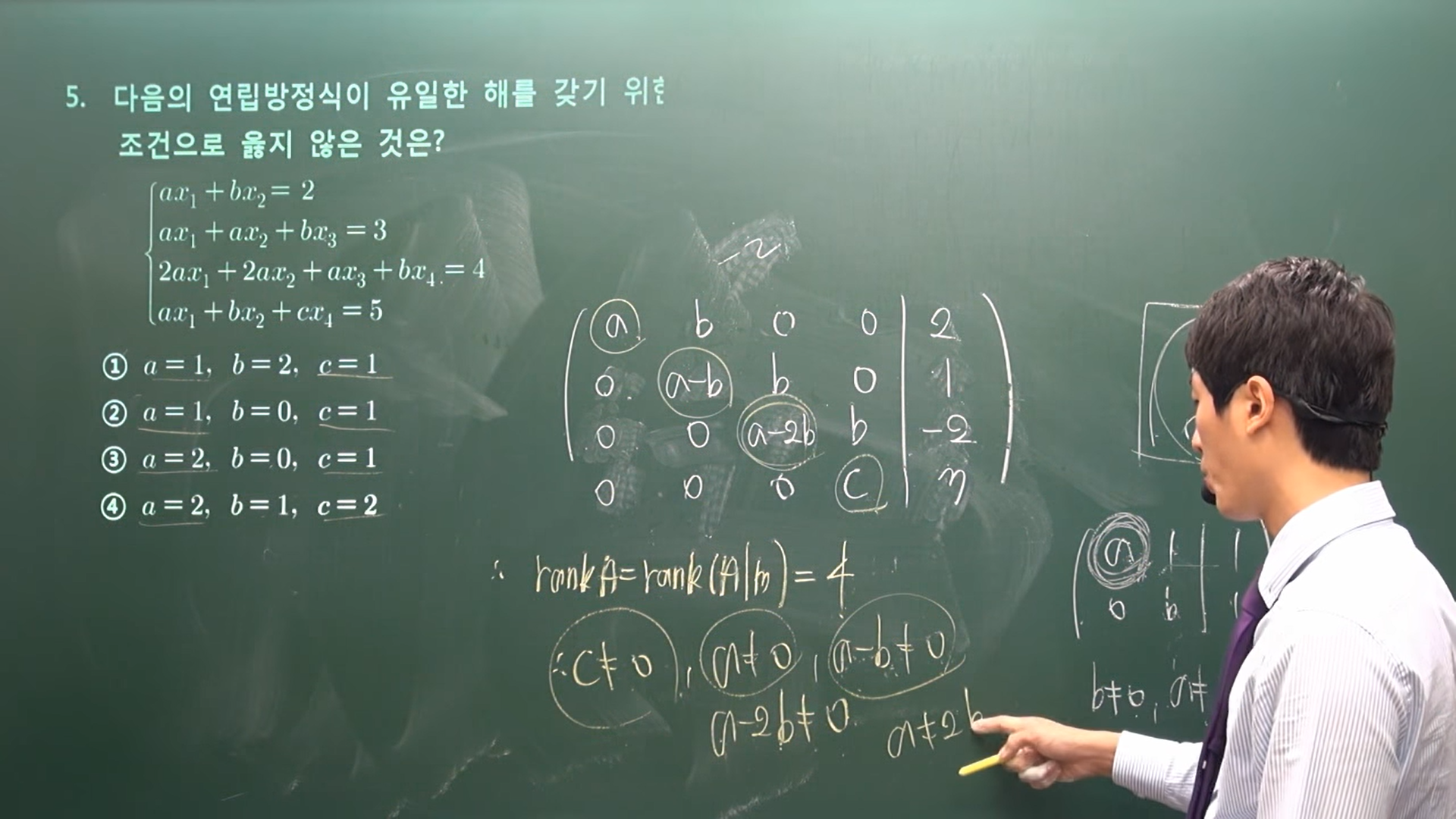 |
| 문제 6 답: -3a-b+c=0 | |
 |
 |
| 해가 존재할 조건 : 해가 1개일 때 + 해가 무수히 많을 때 | |
 |
|
| 문제 7 | |
 |
 |
| 앞에 있는 숫자를 최소 공배수로 맞추어도 상관 없다 | |
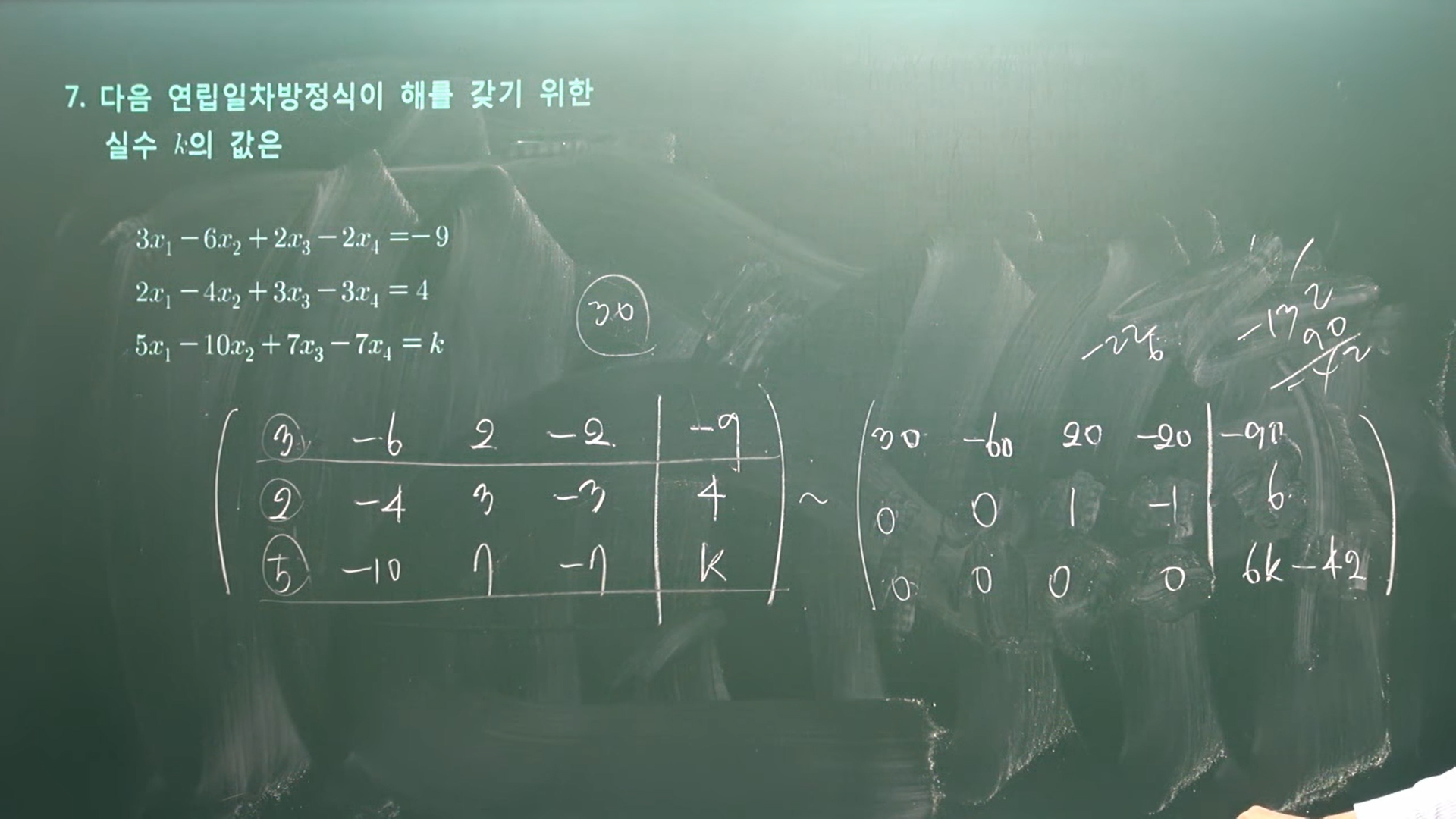 |
 |
| 문제 8 | |
 |
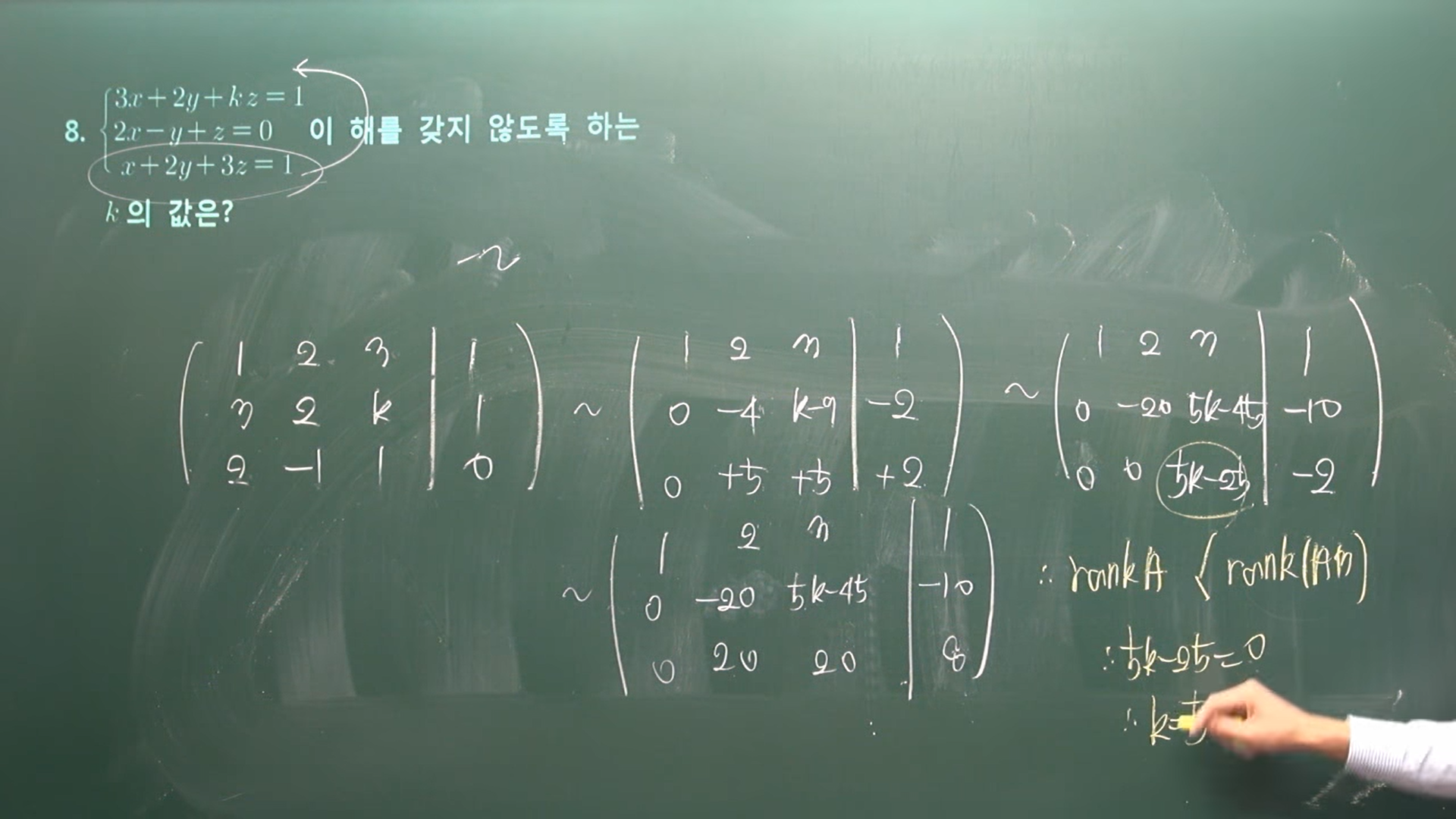 |
| 문제 9 | |
 |
 |
'Memo > 포스코 AI&BD 사전학습' 카테고리의 다른 글
| 선형 대수 - 7강 벡터 공간 및 부분 공간 (0) | 2020.11.03 |
|---|---|
| 선형대수 - 6강 역행렬 (0) | 2020.11.02 |
| 선형대수 - 4강 랭크 (0) | 2020.11.02 |
| 선형대수 - 3강 행렬식1,2 (0) | 2020.11.01 |
| 선형대수 - 2강 벡터의 내적 (0) | 2020.11.01 |