Ch5. DFS/BFS
1. 꼭 필요한 자료구조 기초
- '탐색'
: 많은 양의 데이터 중 원하는 데이터를 찾는 과정으로 대표적인 알고리즘으로 DFS, BFS가 있다.
- '자료구조'
: 데이터를 표현하고 관리하고 처리하기 위한 구조
- 오버플로(overflow) : 특정한 자료구조에 수용할 수 있는 데이터가 가득 찬 상태에서 삽입 연산을 수행할 때 발생
- 언더플로(underflow) : 특정한 자료구조에 데이터가 전혀 들어 있지 않은 상태에서 삭제 연산을 수행할 깨 발생
1-1. 스택
- 선입후출 FILO or 후입선출 LIFO 구조

1-2. 큐
- FIFO 구조
- deque 자료구조를 활용하자. 스택과 큐의 장점을 모두 채택한 것인데 데이터를 넣고 빼는 속도가 리스트 자료형에
비해 효율적이고 queue 라이브러리를 사용하는 것보다 더 간단하다.

1-3. 재귀 함수
- 자기 자신을 다시 호출하는 함수
- 보통 파이썬 인터프리터는 호출 횟수 제한이 있다.
- '재귀 함수의 종료 조건'이 꼭 필요하다.
- 내부적으로 스택 자료구조와 동일하다. 따라서 스택 자료구조를 사용해야 하는 많은 알고리즘은 재귀 함수를 이용하여
간편하게 구현될 수 있다.

- 재귀함수가 수학의 점화식(재귀식)을 그대로 옮겼기 때문에 재귀 함수의 코드가 더 간결하다.
* 수학의 점화식 : 특정한 함수를 자신보다 더 작은 변수에 대한 함수와의 관계로 표현한 것을 의미한다.
2. 탐색 알고리즘 DFS/BFS
2-1. DFS
- 깊이 우선 탐색이라고 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.
- 스택을 이용하는 알고리즘이기 때문에 실제 구현은 재귀 함수를 이용했을 때 매우 간결하게 구현할 수 있다.
- '그래프'
: 프로그래밍에서 크게 2가지 방식으로 표현할 수 있는데 1) 인접 행렬, 2) 인접 리스트이다.

1) 인접 행렬(Adjacency Matrix) : 2차원 배열로 그래프의 연결 관계를 표현하는 방식
- 연결이 되어 있지 않은 노드끼리는 비용이 무한으로 999999999 등의 큰 값으로 초기화한다.

2) 인접 리스트(Adjacency List) : list로 그래프의 연결 관계를 표현하는 방식
- 모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장한다.

3)인접 행렬 vs 인접 리스트
: 메모리 측면에서는 인접 행렬이 낭비되고, 속도 측면에서는 인접 리스트가 느리다.
2-2. BFS
- 너비 우선 탐색이라고 부르며, 가까운 노드부터 탐색하는 알고리즘이다.
- 큐를 이용하면 선입선출이 되기에 자연스럽게 가까운 노드부터 탐색을 할 수 있다.
2-3. DFS vs BFS
- 둘 다 탐색을 수행하는데 O(N)의 시간이 소요된다. 컴퓨터 시스템의 특성상 DFS보다 BFS가 좀 빠르다.
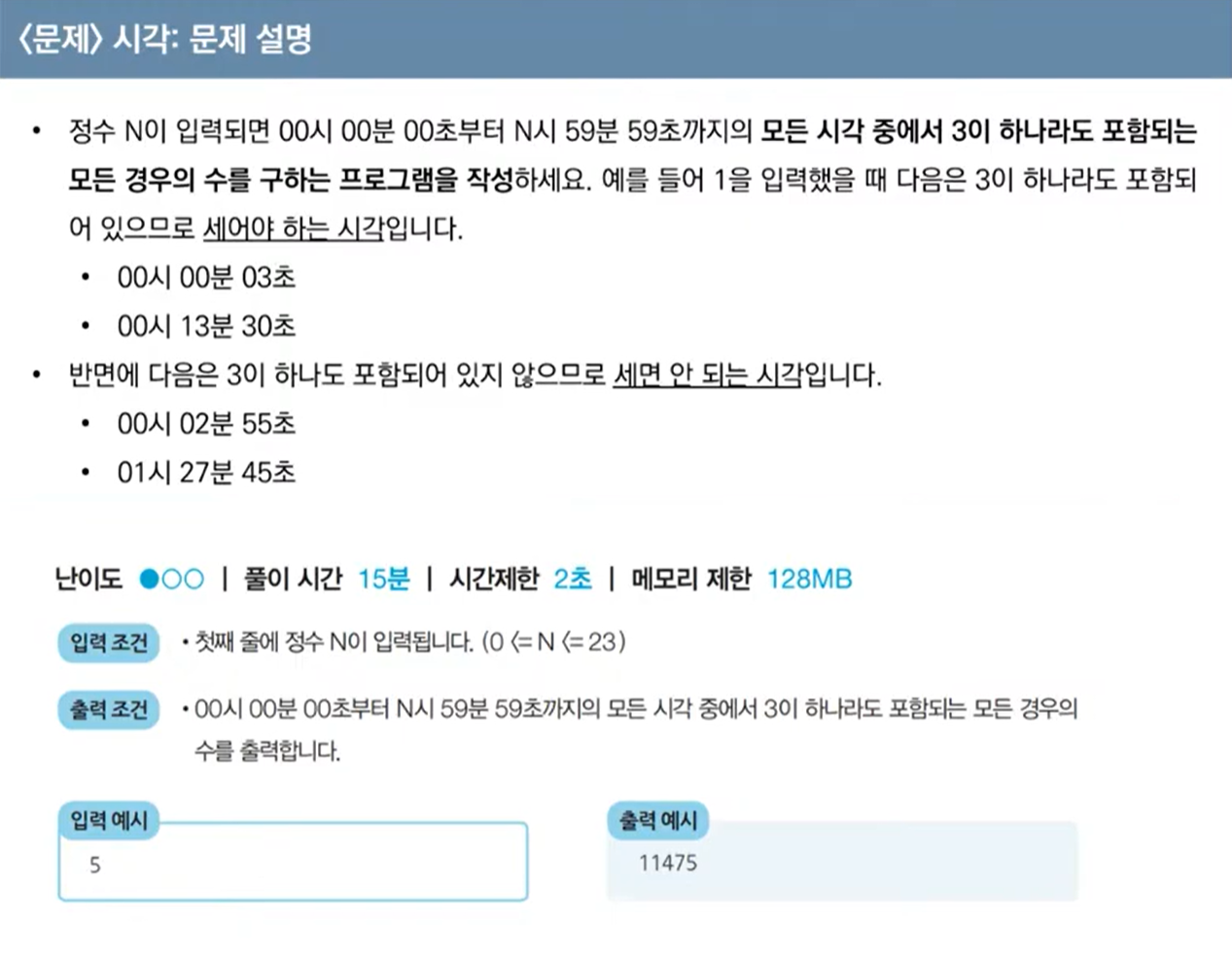
3. 음료수 얼려 먹기
- 문제

- 문제 해결
: 0인 지점에서 주변 상하좌우를 DFS로 방문하면 된다.
- 소스 코드
15 14
00000111100000
11111101111110
11011101101110
11011101100000
11011111111111
11011111111100
11000000011111
01111111111111
00000000011111
01111111111000
00011111111000
11111111110011
11100011111111
11100011111111
11111111111111
n, m = map(int, input().split())
ice_box = []
for i in range(n):
ice_box.append(list(map(int,input())))
def dfs(x, y):
if x <= -1 or x >= n or y <= -1 or y >= m:
return False
if ice_box[x][y] == 0:
ice_box[x][y] = 1
dfs(x-1,y)
dfs(x,y+1)
dfs(x+1,y)
dfs(x,y-1)
return True
return False
result = 0
for i in range(n):
for j in range(m):
if dfs(i,j) == True:
result += 1
print(result)
#include <stdio.h>
using namespace std;
int N, M;
int ice_box[1000][1000];
bool dfs(int x, int y){
if(x <= -1 || x >= N || y <= -1 || y >= M)
return false;
if(ice_box[x][y] == 0){
ice_box[x][y] = 1;
dfs(x - 1, y);
dfs(x, y + 1);
dfs(x + 1, y);
dfs(x, y - 1);
return true;
}
return false;
}
int main() {
scanf("%d %d", &N, &M);
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++)
scanf("%1d", &ice_box[i][j]);
}
int result = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if(dfs(i,j) == true)
result += 1;
}
}
printf("%d\n", result);
return 0;
}
4. 미로 탈출
- 문제
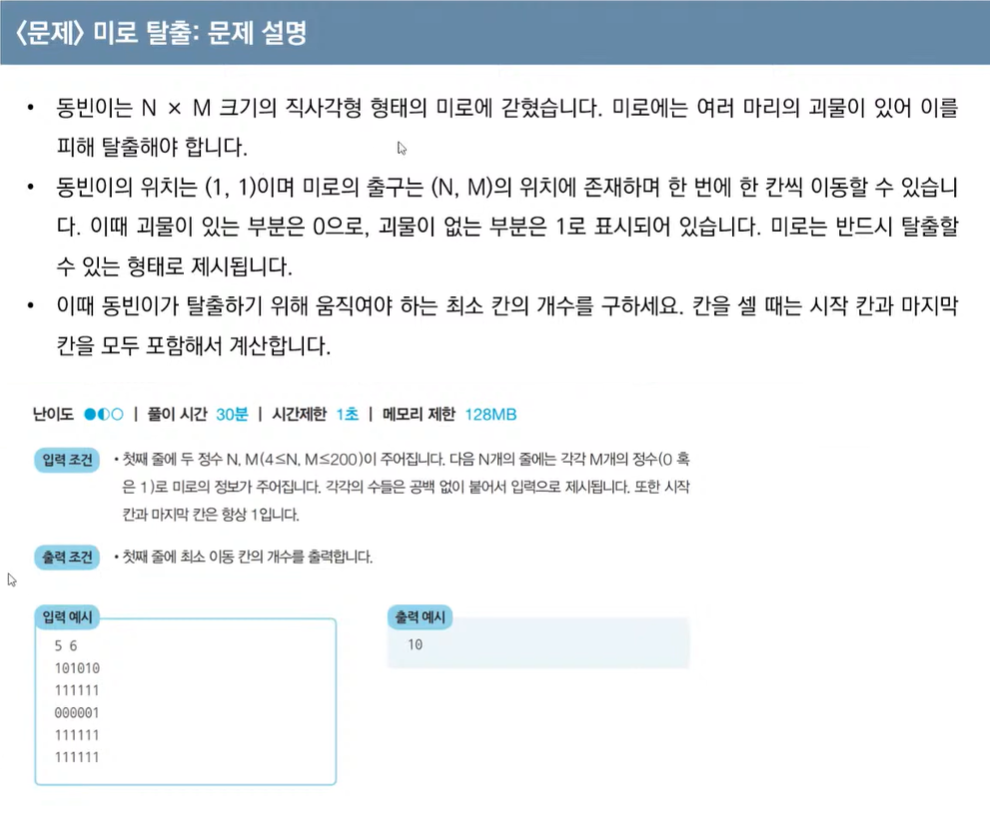
- 문제 해결
: 시작 지점에서 가장 가까운 노드를 차례대로 탐색하는 BFS로 풀면 된다.
- 소스 코드
5 6
101010
111111
000001
111111
111111
from collections import deque
n, m = map(int, input().split())
miro = []
for i in range(n):
miro.append(list(map(int, input())))
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
def bfs(x,y):
que = deque()
que.append((x,y))
while que:
x, y = que.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if nx < 0 or nx >= n or ny < 0 or ny >= m:
continue
if miro[nx][ny] == 0: continue
elif miro[nx][ny] == 1:
miro[nx][ny] = miro[x][y] + 1
que.append((nx,ny))
return miro[n-1][m-1]
print(bfs(0,0))#include <stdio.h>
#include <queue>
using namespace std;
int N, M;
int miro[201][201];
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
int bfs(int x, int y){
queue<pair<int, int>> que;
que.push({x, y});
while(!que.empty()){
int x = que.front().first;
int y = que.front().second;
que.pop();
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if(nx < 0 || nx >= N || ny < 0 || ny >= M) continue;
if(miro[nx][ny] == 0) continue;
if(miro[nx][ny] == 1) {
miro[nx][ny] = miro[x][y] + 1;
que.push({nx, ny});
}
}
}
return miro[N-1][M-1];
}
int main() {
scanf("%d %d", &N, &M);
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++)
scanf("%1d", &miro[i][j]);
}
printf("%d\n", bfs(0,0));
return 0;
}
'Algorithm&Problem > [Algorithm] 이.코.테.다' 카테고리의 다른 글
| [문제실습] Ch 3. 그리디(greedy) (0) | 2021.01.23 |
|---|---|
| [7일차] 이.코.테.다! Ch6 정렬 (0) | 2020.10.02 |
| [5일차] 이.코.테.다! Ch4 구현 Implementation (0) | 2020.09.20 |
| [4일차] 이.코.테.다! Ch3 그리디 greedy (0) | 2020.09.16 |
| [3일차] 이.코.테.다! Ch2 16~20년 코테 기출 유형 분석 (0) | 2020.09.12 |